It is a challenging task to accurately predict the future states of a high-dimensional nonlinear dynamical system in a multi-step-ahead manner, especially with only a short-term time-series data. The major difficulty to solve such a task is the lack of the information, which typically results in the failure of most existing approaches due to the overfitting problem of the small sample size. However, the steady state even for a high-dimensional system is generally constrained to a much lower-dimensional manifold. By exploring such a dynamical property, it has been derived that a high-dimensional system can be equivalently transformed to a low-dimensional dynamics, i.e. a spatiotemporal information (STI) transformation (Fig. 1a). 

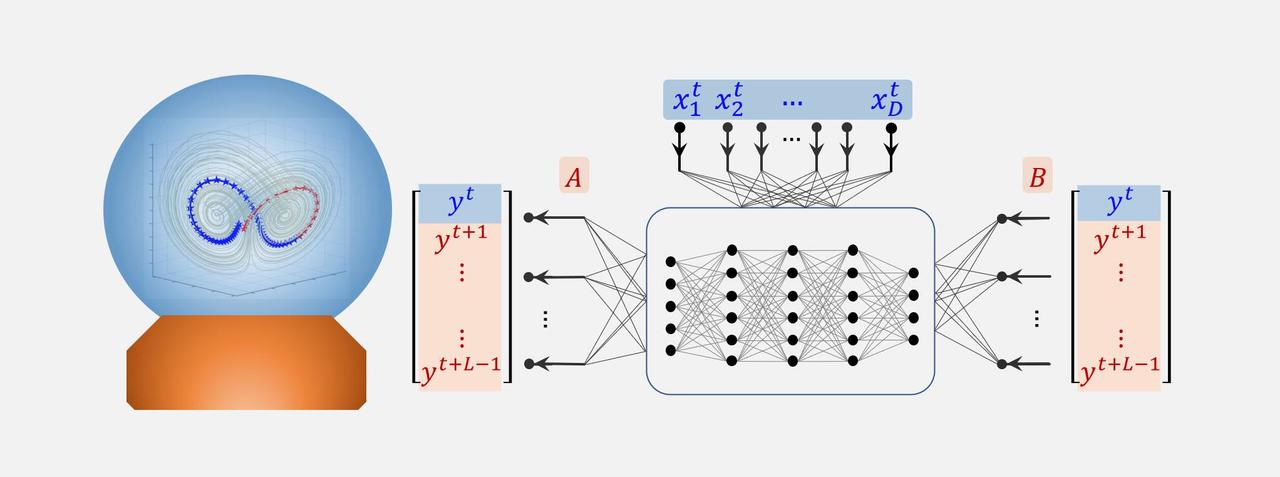
By transforming spatial information to temporal information, we develop an auto-reservoir computing framework: Auto-Reservoir Neural Network (ARNN), to efficiently and accurately make the multi-step-ahead prediction based on a short-term high-dimensional time-series data. Specifically, different from the traditional reservoir computing that uses an external dynamical system irrelevant to the predicted system as a reservoir, we directly take the observed high-dimensional dynamics itself as a reservoir, which maps the high-dimensional data to the future values of a target variable based on both the primary [ AF(X^t) = Y^t ] and conjugate [ F(Y^t) = BX^t ] forms of the STI equations (Fig. 1c), where X^t=(x₁^t, x₂^t,..., x_D^t)′ is the observed high-dimensional state with t=1, 2,..., m,  Y^t=(y^t, y^t+1,..., y^t+L-1)′ is a corresponding delayed vector for any target/to-be-predicted variable y (e.g. y^t=x_k^t) by a delay-embedding strategy with L>1 as the embedding dimension,  A and B are to-be-determined weight matrices satisfying AB=I (I represents an identity matrix), a multilayer neural network F is a nonlinear function (reservoir) in which the weights among neurons are randomly given or fixed in advance. 

By taking advantage of both the reservoir computing structure and STI transformation ARNN achieving the multi-step prediction of the target variable in an accurate and computationally efficient manner. ARNN is performed by simultaneously solving a pair of conjugate STI equations ( AF(X^t) = Y^t  and  F(Y^t) = BX^t ), thus not only solving weights A and B but also obtain the future values of y, i.e., the unknown part {y^m+1, y^m+2,..., y^m+L-1} (the pink area of matrix Y in Fig. 1b). Interestingly, combining the primary and conjugate equations of the STI equations leads to a form similar to that of the autoencoder (Fig. 1d), that is, ARNN encodes X^t to Y^t and decodes Y^t to X^t, where Y^t is the temporal (one-dimensional) dynamics across multiple time points and X^t is the spatial (high-dimensional) information at one time point. Notably, most long-term data, such as expression data from biological systems and interest-rate swaps data from financial systems, may also be regarded as short-term data because those systems are generally not stationary but highly time-varying with many hidden variables. Therefore, to characterize or forecast their future states, it is more reliable to employ recent short-term data, than a long-term series of past data. Therefore, ARNN is a general method suitable for many real-world complex systems even when only recent short-term data are available. 

ARNN provides a new reservoir computing structure for exploring the intrinsic low-dimensional dynamics of the target system, and meanwhile taking advantage of high efficiency of the reservoir computing. ARNN is successfully applied to both representative models and real-world datasets (Fig. 2), all of which show satisfactory performance in the multi-step-ahead prediction, even when the data are perturbed by noise and when the system is time-varying. Actually, such ARNN transformation equivalently expands the sample size and thus has great potential in practical applications in artificial intelligence and machine learning.

For more information, please see our paper:

Pei Chen, Rui Liu, Kazuyuki Aihara, Luonan Chen. Autoreservoir computing for multistep ahead prediction based on the spatiotemporal information transformation. Nature Communications 11, 4568 (2020). https://doi.org/10.1038/s41467-020-18381-0